센서간 캘리브레이션 개요
- 선행학습 : 카메라 intrinsic parameter ( 카메라 왜곡계수, focal length 등)
- 참조 : Direct Linear Transformation - gaussian37 (Homography 관련)
- 참조 : Stereo Camera Calibration and Triangulation with OpenCV and Python (temugeb.github.io) (stereo 카메라 캘리브레이션 관련, 좌표계 곽련)
- 참조 : 다크 프로그래머 :: [영상 Geometry #1] 좌표계 (tistory.com) (좌표계 관련)
- 참고 : 다크 프로그래머 :: 카메라 캘리브레이션 (Camera Calibration) (tistory.com) (카메라 intrinsic parameter)
본 글에서는
1. 이미지(2D)안에서의 homography에 대한 개략적인 설명
2. 카메라 캘리브레이션(intrinsic parameter)
3.카메라-카메라 , 라이다-카메라 센서간 캘리브레이션(multi-sensor calibraion)
4.실제 캘리브레이션 과정 서술
1.homograpy (2D 이미지 변환)
(최소) 4개의 대응점을 이용하여 3*3 이미지 변환 행렬을 찾는 것
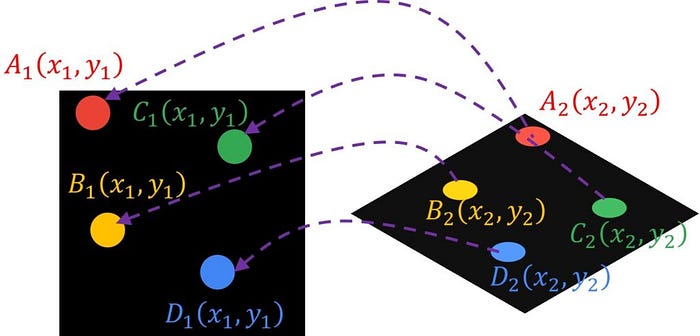

- 특정 이미지 (x,y)픽셀에 대응하여 (x`,y`)로 변환하는 수식
H를 homograpy 행렬이라고 한다. h9의 경우 스케일에 관련된 값으로 보통의 경우 1을 사용
8개의 미지수를 찾기 위해 8개의 연립 방정식이 필요하다
행렬식을 정리하고, 4개의 점 (x1, y1) ~ (x4,y4), (x`1, y`1) ~ (x`4,y`4) 으로 연립방정식을 세워보자
4개의 대응되는 지점의 총 8개의 좌표는 이미 선행적으로 구해져 있어야 한다



위 식을 0으로 만들어주는 H 행렬을 구해줘야한다. 이 때 SVD를 이용하여 singular value가 가장 작은 값에 해당하는 right singular vector가 H가 된다 (이에 대한 상세한 내용 및 수학적 증명은 파일 참고)
이 때 구해진 H 행렬을 이용해 이미지를 변형할 수 있다
또한 stereo 카메라의 얕은 의미의 캘리브레이션도 가능하다. 왜냐하면 두 카메라 간 homograpy를 알 고 있다면 대응점 찾는것이 가능하다. 따라서 1번 카메라의 특정 객체의 픽셀 위치를 이용해 2번 카메라에서 어느 픽셀에 해당 객체가 있는지 계산 가능하다
2.카메라 intrinsic parameter 캘리브레이션
카메라 intrinsic parameter는 크게 다음과 같다 (intrinsic parameter 관련 내용은 다크프로그래머님의 블로그 참고)
- f_x(x축 focal length)
- f_y(y축 focal length)
- c_x(x축 주점)
- c_y(y축 주점)
- skew_c(비대칭 계수, 0으로 간주)
- distortion 파라미터
6번의 경우 일반적으로 포함하지 않지만, 필수적으로 구해야하는 값이기에 포함하였다. 카메라 캘리브레이션 과정은 핀홀카메라를 가정하고 계산하는데 현대 카메라는 렌즈를 사용하기 때문에 왜곡(distortion)이 있다. 따라서 이를 보정한 뒤 캘리브레이션을 진행해야 한다. 왜곡 보정 관련 내용은 링크 참조


(u,v)카메라 픽셀좌표계의 좌표이며, x_w, y_w, z_w는 3차원 월드 좌표계 상의 좌표이다
P11 ~ P34는 이를 변환할 수 있는 행렬인 것이다
캘리브레이션 보드를 찰상할 때에, 캘리브레이션 보드 왼쪽 아래 코너의 픽셀 위치를 찾아낼 수 있을 것이며(checkerboard detection)
월드 좌표계상에서의 위치도 알 수 있다. 왜냐하면,
1.캘리브레이션 보드를 평면으로 가정한다 (z_w = 0)
2.캘리브레이션 보드 왼쪽 아래 코너를 (0,0,0)로 지정한다
3. 캘리브레이션 체크무늬의 실제 크기값을 측정해 파라미터로 넣어준다 (ex: 3.19cm)
intrinsic parameter만 구할때에는 실제크기값을 알 필요 없다. 실제 크기를 다르게 넣으면 R,t가 바뀌게 되지 intrinsic은 바뀌지 않는다
따라서 P 행렬의 값만 구하면 된다
P 행렬의 경우 위에서 Homography 행렬을 구한것과 같은 방식으로 구한다
(x_w, y_w,z_w) 좌표들은 캘리브레이션 보드의 교차점의 월드 좌표를 이용하면 된다

3차원 좌표를 2차원 이미지에 투영하는 공식에 따라, P행렬은 아래와 같다



M_int = 카메라 intrinsic parameter
M_ext = 카메라 extrinsic parameter (r = rotation, t = traslation)
P 3열까지만 분리해서 봤을때, intrinsic parameter * Rotation 으로 정리된다.
intrinsic parameter(K)는 상삼각 행렬이며 R을 회전행렬으로써 orthonormal 행렬이다
따라서 QR decomposition을 응용한 RQ decomposition(이때 R은 rotation이랑 다른 의미임)이 가능하며 intrinsic parameter(K) * 회전행렬(R)로 분리된다.
P 4열의 경우 intrinsic parameter* translation의 곱이다.
방금 전 과정에서 intrinsic parameter(K)를 구하였으므로이동행렬t의 값을 구할 수 있다

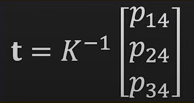
이로써 캘리브레이션 보드를 이용한 카메라 intrinsic parameter 추출을 완료하였다
3.센서 간 캘리브레이션(multi-sensor calibration)
센서들의 데이터를 월드 좌표계로 변환한 뒤 기준 센서의 좌표계에 대한 대상 센서의 rotation, traslation 행렬을 구하는 것
*카메라-카메라 extrinsic parameter 캘리브레이션
intrinsic parameter 캘리브레이션 과정에서 회전행렬(R)과 이동행렬(T)이 구해졌었다
이때의 R,T의 의미는 카메라 좌표계와 월드좌표계(캘리브레이션 보드 맨왼쪽하단 코너) 의 관계라고 할 수 있겠다
카메라-카메라(stereo 카메라) 캘리브레이션에서는 카메라 간 R,T를 구하는것이 핵심이다
내부 캘리브레이션 과정에서 구했던 R,T를 이용하여 카메라 간 변환행렬을 구하는 방법을 생각해볼 수도 있다
하지만 변환행렬을 곱해서 구하는 건 오차가 커지는 방법이다(짐벌락 문제, 오차의 누적)
[R2|T2] * [R1^-1|-T1] = [R|T]
[R1|T1] 1번 카메라 좌표계에서 바라본 월드좌표계의 위치, 월드좌표계에서의 1번카메라좌표계 방향
[R2|T2] 2번 카메라 좌표계에서 바라본 월드좌표계의 위치, 월드좌표계에서의 2번카메라좌표계 방향
* R과 t는 각각 어떻게 해석해야 하는가?
R : 우측(2번)카메라 좌표계에서의 좌측(1번)카메라 방향(orientation)
t : 좌측(1번)카메라 좌표계에서의 우측(2번)카메라 위치
아래 식을 계속 묵상하다보면 의미가 이해된다. 아래 결과값은 카메라의 위치가 아니라 카메라 좌표계에서의 대상 포인트의 위치이다.
x_1 = R *x_2 + t
예시)
| 1 0 0 0 | | 1 | | 1 | | 0 1 0 0 | | 1 | | 1 |
| 0 1 0 0 | x | 1 | = | 1 | | -1 0 0 0 | x | 1 | = |-1 |
| 0 0 1 3 | | 1 | | 4 | | 0 0 1 0 | | 1 | | 1 |
| 0 0 0 1 | | 1 | | 1 | , | 0 0 0 1 | | 1 | | 1 | (z축 90도 회전)
Epipolar geometry
참고 : Epipolar Geometry | Uncalibrated Stereo - YouTube
참고 : [MVG] Stereo Camera Calibration 예제코드 및 설명 (C++) (tistory.com
동일한 지점에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A,B의 기하학적 관계를 일컫는다
essention matrix와 fundamental matrix를 구하는데에 활용한다
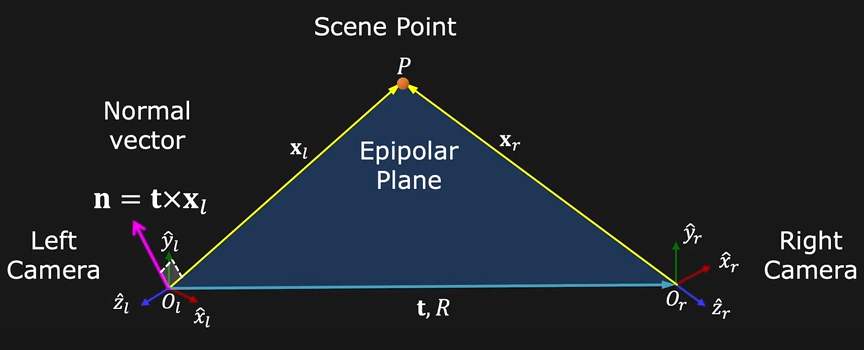

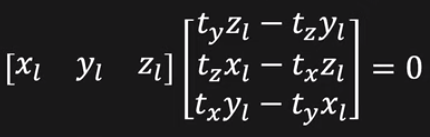

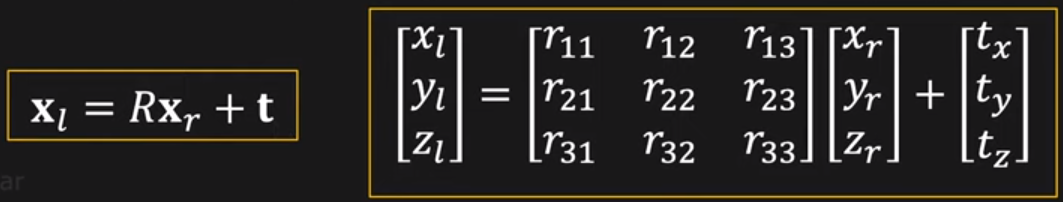



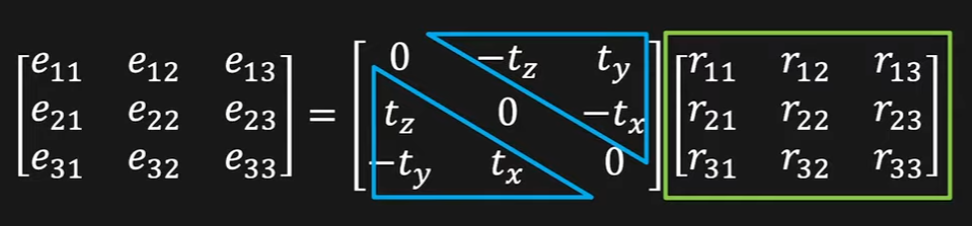
Tx의 전치행렬 = -Tx인 형태(skew-symetric matrix)이므로 Tx는 SVD를 이용해 구할 수 있다.
E = UΣV^T에서, t = U_3(U의 마지막 열)이다. 수학적 증명은 링크에서 essential matrix 참조
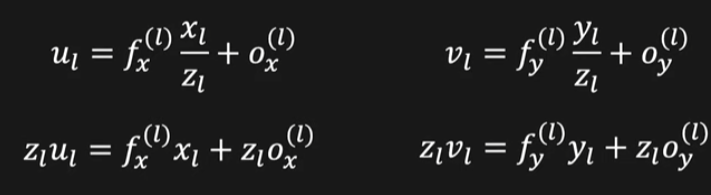
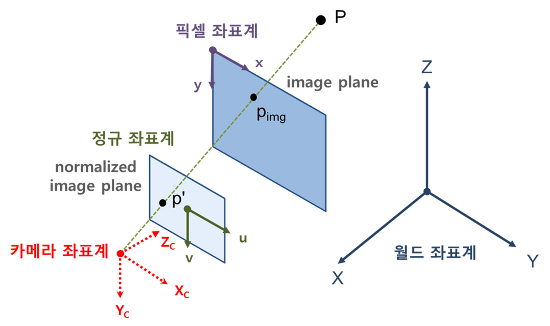
u,v는 픽셀좌표계 값이다. 월드좌표계 각을 픽셀 좌표계로 변환하는 과정


픽셀좌표계 = K * 카메라좌표계 이다. 이는 3차원 정보를 2차원 정보로 변환하는 과정이다.
이때 K(intrinsic parameter)는 이미 알고있다(2.카메라 intrinsic parameter 캘리브레이션 참고)


월드좌표계 값을 픽셀좌표계 값으로 변환하여 정리를 계속한다. 이때 z항은 카메라 좌표계 상에서 전면으로 부터의 거리 값인데 이미지에 보여지는 포인트에 대해 카메라 좌표계의 z값은 항상 0일 수밖에 없다(z=0은 카메라 렌즈의 위치)
따라서 K항들과 E를 연산하여 F행렬을 만든다(Fundamental matrix)
이제 F 행렬을 알면 카메라 간의 R,T를 알아낼 수 있다
K는 카메라 intrinsic parameter로 이미 구해졌으며, SVD를 이용해 R,T를 분해해낸다
$$E = K_l^\intercal FK_r$$
$$E = T_XR$$


동일한 객체에 서로 다른 viewpoint에서 찍은 사진에서 특징점을 8개 선정한다
이 픽셀 좌표계에서 정의된 좌표 값들을 대입하여 LLS(linear list square)문제로 만든 뒤 SVD를 이용해 푼다
(homogenous coordinate이기 때문에 f_33=0이다)
(f = singular value가 가장 작은 값에 해당하는 right singular vector ,homograpy에서 사용된 방법과 동일)
다만, intrinsic parameter K가 구해져있다는 가정하에, F까지 계산할 필요 없이 E만을 이용하여( 픽셀 좌표계가 아닌 월드 좌표계) R,t를 산출하는것도 가능한 것으로 확인된다. E를 구하는 방법은 F를 구하는 방법과 유사하다
카메라-카메라 캘리브레이션 과정 요약
- 8개의 point를 이용해 F를 구한다
- E = K^T * F * K를 이용해 E를 구한다
- E = T_x * R을 이용해 R,t를 구한다
*카메라-라이다 extrinsic parameter 캘리브레이션
카메라-카메라 캘리브레이션을 충실히 이해했다면 카메라-라이다 캘리브레이션도 쉽게 이해할 수 있다.
2.카메라 intrinsic parameter 캘리브레이션에서 보았듯이, 체커보드를 이용하면 단안카메라로도 3차원 좌표를 특정할 수 있다(이때 구해지는 이동 행렬) 그리고 라이다의 경우 바로 3차원 좌표들이 구해진다.
이 두 센서의 3차원 좌표들을 일치시키는 과정이 카메라-라이다 캘리브레이션이다.
이때 Fundamental Matrix까지는 구하지 못하며(라이다른 카메라 모델링이 안되므로) Essential matrix을 구하고, 이를 R,t로 분해하는 방법이 가능하다.

그러나 실제 적용 방법은 매우 다양하다(target less, circular target.. etc). 그 중 MATLAB에서 사용되고 있는 방법론(논문)을 설명하겠다.
참고 : 라이다 및 카메라 보정 - MATLAB & Simulink - MathWorks 한국
기본적으로 이미지와 point cloud에서 체커보드를 봤을때, 법선을 그을 수 있을 것이다. 이 법선 벡터를 일치시키고, 위치도 일치시키면 R,t를 구할 수 있는 것이다.
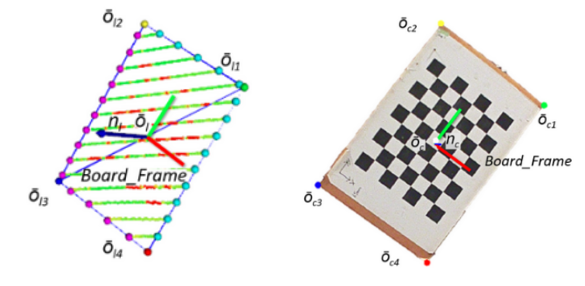
point cloud에서 법선을 찾을때는 3d ransac을 이용해 평면을 먼저 찾는다. 평면을 찾게 되면 법선은 자동으로 찾아지게 된다
이미지에서는 PnP알고리즘을 이용해 보드의 자세를 추정하고, 패턴을 함께 인식하여 법선을 추정한다
R,t는 각각 3자유도이다. 각 자유도마다 최적화를 시키며, 다시 함께 최적화를 하는 방법을 쓴다. 이때 유전 알고리즘을 사용한다.
4.실제 캘리브레이션 과정
*RGB카메라-열화상카메라 캘리브레이션
RGB 카메라 : 국내 S社
열화상 카메라 : 국내 H社
대형 체커보드는 사이즈 20cm
열화상 intrinsic 체커보드 사이즈 4cm
*opencv를 이용한 stereo calibration
참고 : Stereo Camera Calibration and Triangulation with OpenCV and Python (temugeb.github.io)
*열화상 카메라 intrinsic 캘리브레이션
opencv에서 체커보드는 border가 필요하다 [링크].
열화상 카메라의 경우 온도가 높을수록 intensity 값을 높인다( 하얀색). 검은색 무늬가 열화상 카메라에선 하얀색으로 보인다.
이때 border(경계)부분이 검은색으로 나오게 되는데 이러한 현상이 체커보드 무늬를 찾지 못하게 하는듯 하다. 따라서 열화상는 이미지를 반전시켜서 진행해야한다
열화상 카메라가 체커보드를 인식할 수 있게 전등같은걸 갖다대어 온도를 높이거나 야외 직사광선 아래에서 진행하면 색깔간에 온도차이가 생기기 때문에 체커보드를 인식할 수 있게된다



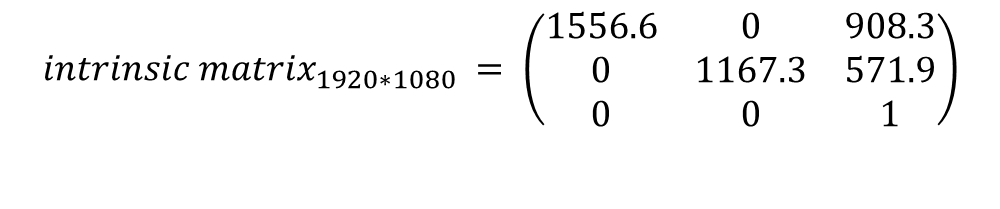
이 때, 열화상 카메라와(640*480) RGB 카메라의(1920*1080) 해상도가 다르므로 열화상 이미지를 RGB에 맞게 resize 해주고, intrinsic 역시 비율에 맞게 증가시켜준다. (distortion은 그대로)
*RGB 카메라 intrinsic 캘리브레이션



*stereo calibration

체커보드 인식방향이 서로 다를때에는 제외시켜야 한다[참고링크]




*MATLAB을 이용한 stereo calibration 결과
*열화상 카메라 intrinsic 캘리브레이션



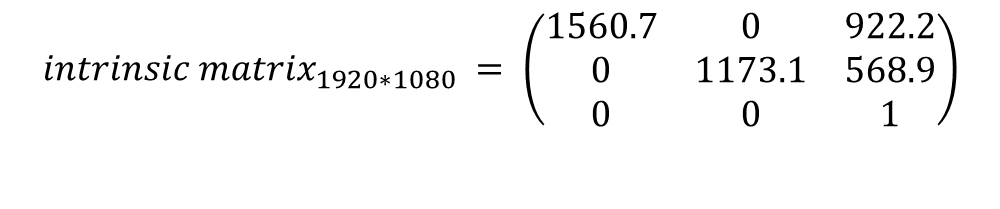
*RGB 카메라 intrinsic 캘리브레이션

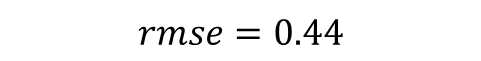

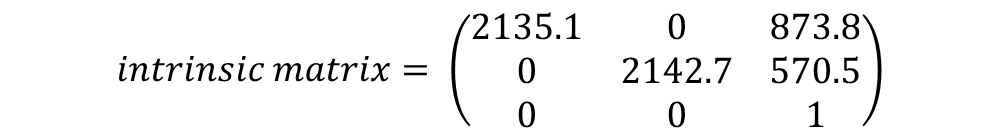
*stereo calibration





*카메라-라이다 캘리브레이션
라이다 : Ouster社 OS2-128
카메라 : 국내 M社 개발품
핵심은 카메라와 라이다 간 이동행렬(T), 회전 행렬(R)을 찾아내어
한쪽 데이터를 다른 데이터에 투영 or 데이터 정합을 이루는 것이다.

LiDAR-Camera calibration을 하기 전에 선행적으로 Camera의 distortion값과 intrinsic parameter를 구해야한다.



이후 카메라와 라이다 데이터를 동시 취득한다
실험 조건
역광 x 주변에 반사되는 물체 x 주변에 움직이는 물체 최대한 x
거리 바꿔가면서 취득, 체커보드 기울인 데이터도 취득
데이터 28개 이상


참고 : https://github.com/ccyinlu/multimodal_data_studio




후기, 디스커션
센서 간 캘리브레이션의 경우 이론만 안다고 되는건 아니다. 실제 카메라의 특성, 체커보드의 스펙이나 찍는 환경에서 영향을 받는 경우도 많다. 어떤 언어, 어떤 툴을 쓰냐에서도 차이가 생긴다.
opencv에서는 캘리브레이션 보드에 마진이 있어야 인식을 한다[링크]. MATLAB에서는 없어도 된다.
opencv와 MATLAB은 왜곡계수를 나열하는 순서가 다르다
opencv와 MATLAB에서 체커보드를 인식할 수 있는 성능, 조건이 다르다
캘리브레이션 작업을 원할히 수행하기 위해서는 이론적 배경을 갖춤과 동시에 실제 캘리브레이션 과정을 다양하게 수행해보는게 좋은 것 같다. 이 캘리브레이션 방법론에 정답이 있는 것도 아니며, 수십가지의 방법이 있기 때문에 그 중 자기에게 맞는 방법을 찾아서 루틴화 하는것이 좋다
실제 현장에서는 아주 깔끔한 센서 세팅이 쉽지 않다.
해상도가 서로 다른 경우라던가, 카메라의 품질이 좋지 않는 경우도 있다.
그때마다 방법은 있으니, 포기하지 않고 이미 정리가 잘된 문서라던가, 이론적 배경을 바탕으로 문제를 해결해 나가려는 태도가 중요하다.
실제 운행중에 센서간의 R,T가 바뀔 위험도 있기에 이를 수시로 체크하는 과정도 중요하다.
이를 방지하기 위해 주기적으로 taget less 캘리브레이션 과정을 운용중에 할 수 있도록 자동화 하는것도 괜찮을것 같다.
카메라의 경우 화각에 따라 fisheye model을 쓸것인지, pinhole model을 쓸것인지도 잘 생각해야한다. 필자의 경우 60도, 120도 카메라 캘리브레이션 경험이 있는데 각각 다른 모델을 사용하였다.
왜곡 계수가 캘리브레이션 과정에서 언급이 안되는 경우가 많은데 매우 중요한 부분이다. 왜곡계수를 몇개 쓸것인지도 잘 세팅해야한다.
타 센서간 캘리브레이션을 하면 데이터 전체 영역에서 완벽히 매칭이 되는 경우는 드문것 같다. 이런 부분을 최소화 하기 위해 꼼꼼히 하던지 혹은 센서 융합 영역을 제한하는 방법을 사용하는게 좋을성 싶다
센서에 대한 이해가 꽤 있어야 한다. 라이다 point cloud의 경우 생각처럼 잘 나오지 않기 때문에 당황할 수 있다. 예컨데 반사도가 높은 영역과 낮은 영역이 나란히 있을때, 높은 영역이 약간 볼록해지는 현상이 있다. 카메라 역시 화각이나 센서 품질에 캘리브레이션 결과가 영향을 받을 수 있다. 광각 카메라의 경우 이미지의 모서리 상 하 좌 우에서 왜곡이 심해지고 초점이 흐려지는 경우도 있다. 이를 잘 파악해서 보완을 하던지, 적어도 문제인식을 하고 있는것이 필요하다.